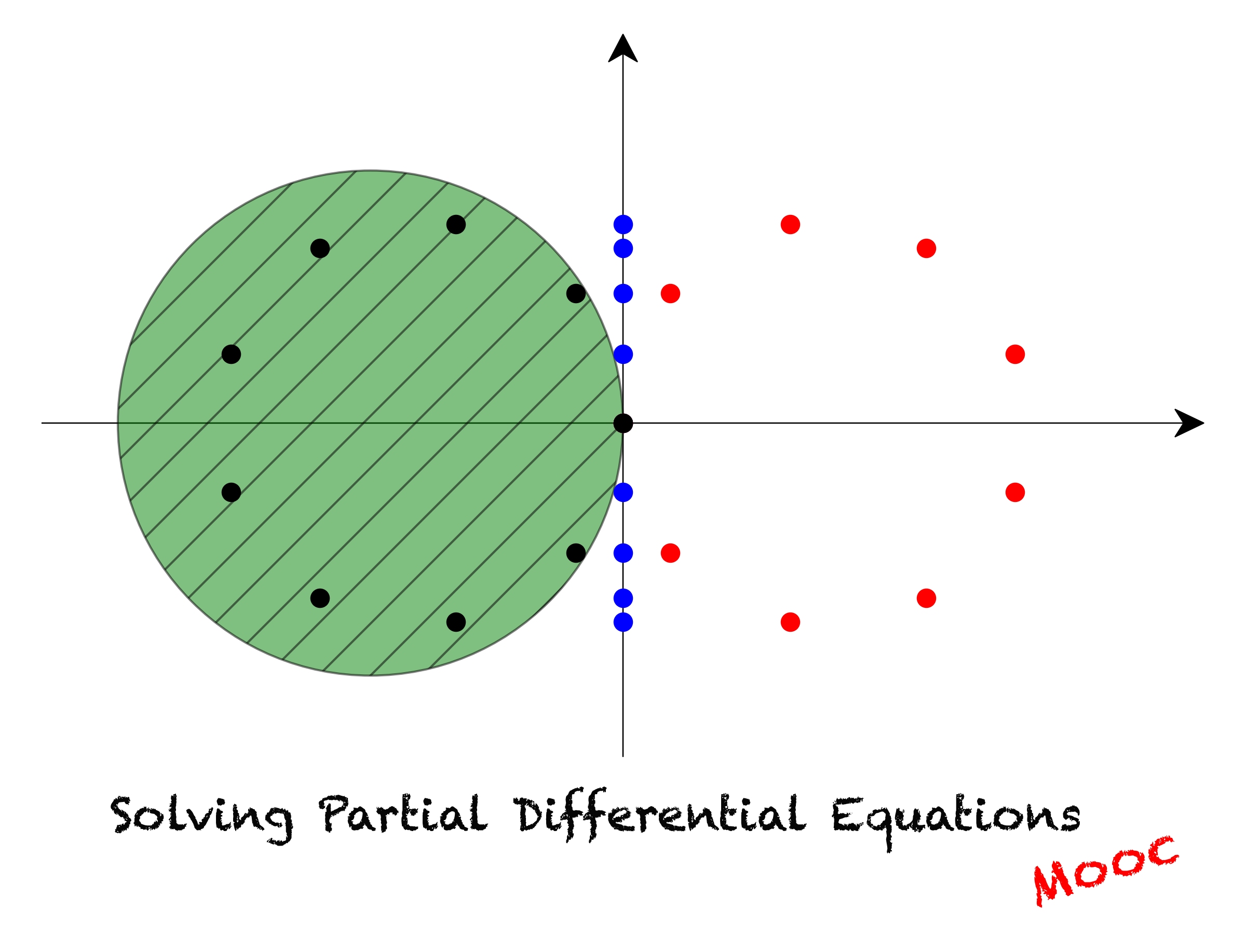
— in this section we will discuss implicit differentiation. Not every function can be explicitly written in terms of the independent variable, e. g. Y = f (x) and yet we will still need to. The partial derivative of f with respect to x at (a; This tells us the instantaneous rate at which f is changing at (a; B) when we move parallel to the x. — implicit differentiation of a partial derivative. Asked 6 years, 10 months ago. Modified 6 years, 10 months ago. If z is defined implicitly as a. Implicit differentiation by partial derivatives calculate dy/dx if y is defined implicitly as a function of x via the equation 3x^2−2xy+y^2+4x−6y−11=0. Partial derivatives examples and a quick review of implicit differentiation. The kids are taught to differentiate implicitly, then solve for dy dx d y d x. I remembered that you could set the original equation equal to some function g g, and simplify with this formula (from. How to do implicit differentiation. Differentiate with respect to x. Collect all the dy dx on one side. Solve for dy dx. X 2 + y 2 = r 2. Differentiate with respect to x: D dx (x 2) + d dx. — here is a set of practice problems to accompany the implicit differentiation section of the derivatives chapter of the notes for paul dawkins calculus i course at lamar. This section extends the methods of part a to exponential and implicitly defined functions. By the end of part b, we are able to differentiate most elementary functions. Our mission is to improve educational access and learning for everyone. Openstax is part of rice university, which is a 501 (c) (3) nonprofit. Give today and help us reach more students. Z are related implicitly if they depend on each other by an equation of the form f (x; Z) = 0, where f is some function. For example, the points on a sphere centred at. Fortunately, the concept of implicit differentiation for derivatives of single variable functions can be passed down to partial differentiation of functions of several variables. — we use implicit differentiation to find derivatives of implicitly defined functions (functions defined by equations). By using implicit differentiation, we can find the equation of a. — implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between the variables is given implicitly rather than explicitly. — implicit differentiation is a technique based on the chain rule that is used to find a derivative when the relationship between the variables is given implicitly rather than. Let g(x, y) =x2y4 − 3x4y g ( x, y) = x 2 y 4 − 3 x 4 y. (i) find the first partial derivatives gx g x and gy g y. (ii) using (i) above, find dy dx d y d x. (iii) if g(x, y) = 0 g ( x, y) = 0, confirm your. To find the implicit derivative, take the derivative of both sides of the equation with respect to the independent variable then solve for the derivative of the dependent variable with respect to the. How to find partial derivatives of an implicitly defined multivariable function using the implicit function theorem, examples and step by step solutions, a series of free online calculus. — in this section we will the idea of partial derivatives. We will give the formal definition of the partial derivative as well as the standard notations and how to compute them in practice (i. e. Without the use of the definition). — when you perform implicit differentiation, you start off by assuming that there is such a function and then differentiate both sides of the equation f(x, y) = 0 f (x, y) = 0 taking. — this calculus 3 video tutorial explains how to perform implicit differentiation with partial derivatives using the implicit function theorem. • area of a. Learn how to find and interpret the partial derivatives of multivariable functions, and how they relate to tangent planes and linear approximations.